反比例のグラフの問題

1年

難易度☆☆

この問題は、反比例のグラフを利用した図形問題です。

ことができれば、解ける問題です。
ぶっちゃけ「反比例とは何か？」がわかっていなくても解けます。

関数とは、一言でいうと数字の変換器です。

関数に数字を入力すると、他の数字に変換されて出力されます。変換した結果たまたま同じ数字になることもあります。

例えば、$y=2x-1$という関数の$x$の部分に3を入力してみましょう。すると、$$y=2\times3-1\\=6-1\\=5$$となり、$y=5$が出力されることがわかります。

このように、関数の文字の代わりに数字を入れてみることを「代入する」といいます。
同じ関数に同じ数字を入力すると、必ず同じ数字が出力されます。
(ただし、関数の種類によっては出力が同じでも入力が同じとは限らないことを知っておくと良いでしょう。)

ここで、関数のグラフについても説明しておきましょう。

グラフは、関数の入力と出力の関係を図で表したものです。

先ほど例にあげた$y=2x-1$という関数のグラフは、以下のようになっています。

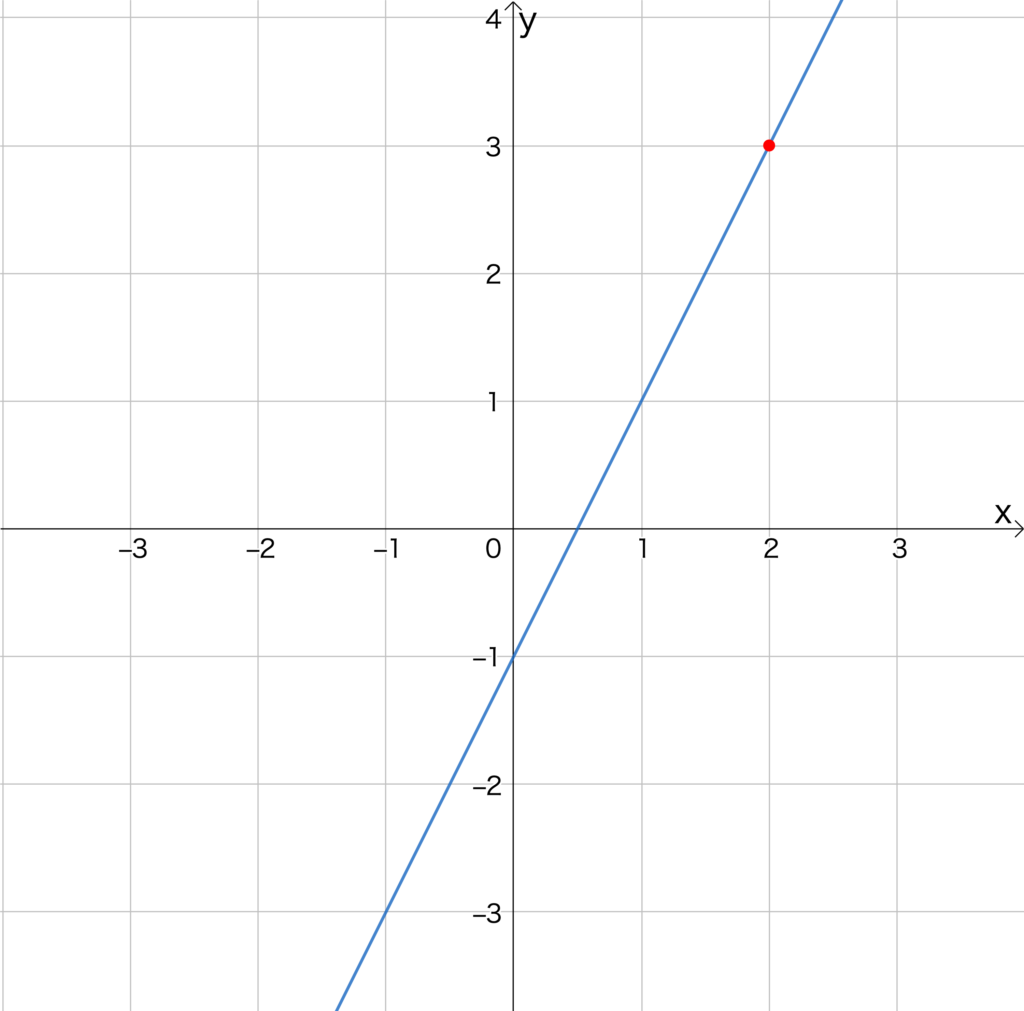
この図のうち青い直線が関数$y=2x-1$のグラフですが、グラフの説明をする前に二つの矢印と赤い点を見てください。

$x$という文字がくっついた矢印をx軸、$y$がくっついた矢印をy軸と呼びます。

そして、x軸上の2のところに縦に引いた直線と、y軸上の3という数字のところに横に引いた直線が交わった場所に赤い点があります。

これは、$x=2$を入力すると$y=3$になるということを表しているのです。

さて、今回は$x=2$、$y=3$を例に見てみましたが、当然$x$が変われば$y$は別の数字になります。
$y=2x-1$の$x$にいくつか数字を代入して、$y$の値を実際に計算してみましょう。
$x$や$y$は少数や分数、マイナスの値も取ることができるので、

というように、無限に点を増やすことができます。

実際に今のように点をたくさん計算して描きこんでいくとわかりやすいのですが、こうして点を無限に増やしていくと直線になりそうな気がしませんか…？

なるのです！

その直線こそが、青線で示された直線であり、関数$y=2x-1$のグラフということになります。

テストでは、関数のグラフはよく図形問題と合体して出題されます。

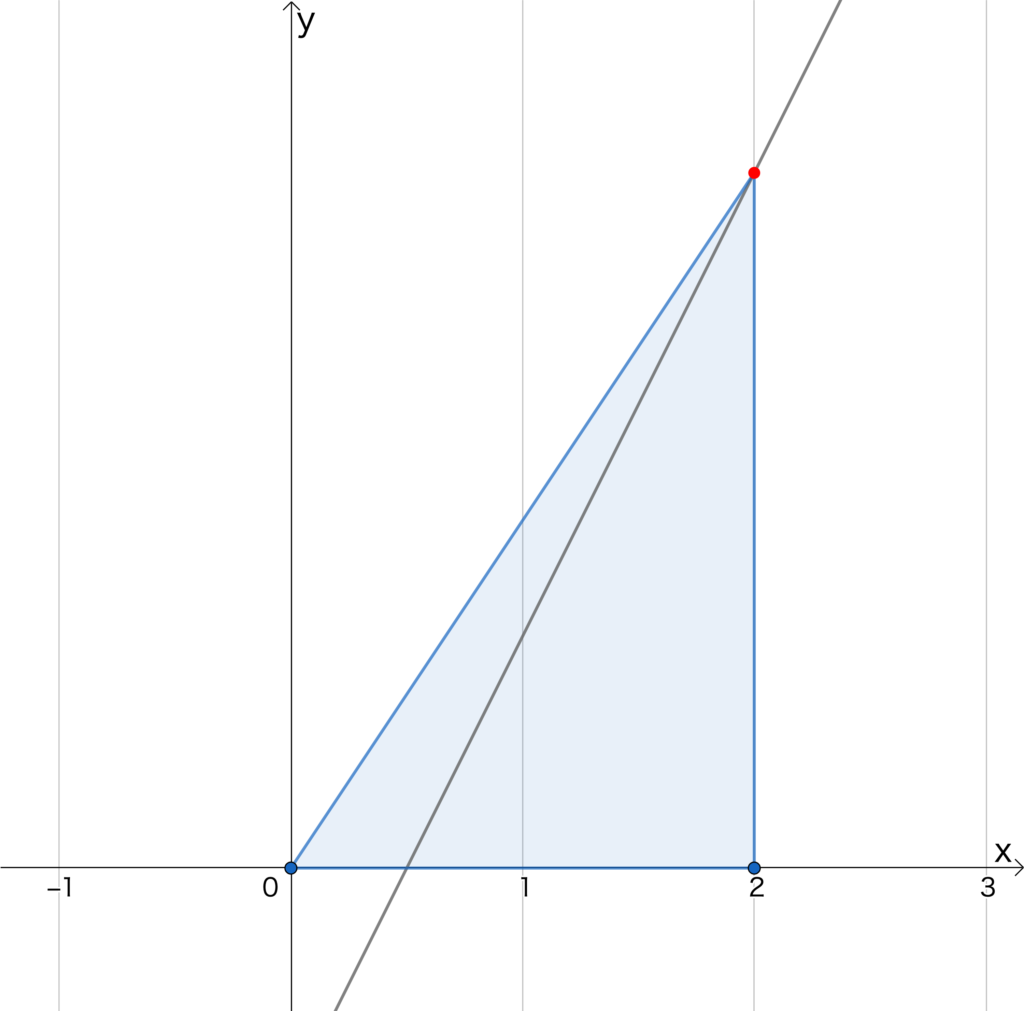
関数$y=2x-1$のグラフ上に、$x=2$となる点をおきました。この点と、点から真下に下ろしたx軸上の点、そして原点($x=0,\ y=0$の点)を結ぶと、図のような三角形ができます。この三角形の面積はいくらでしょうか。

三角形の面積を求めるには、その三角形の底辺と高さを知る必要があります。

底辺は、$x=0$の点から$x=2$までの長さなので、2であるとわかります。

でも、最初においた点の$y$座標が分からないので、高さを求めることができません。こんな時にはどうすればいいのでしょうか？

この問題は、点が$y=2x-1$のグラフ上にあることを考えると解決できます。
$y=2x-1$のグラフは、入力と出力の関係を表す点の集まりだからです。
今回おいた点も、そんな無数にある点のうちの一つを選んだだけなのです。

つまりこの点のx座標とy座標は$y=2x-1$の入力と出力の関係を満たしているはずなので、$x=2$を代入すると、$y=3$であることがわかります。

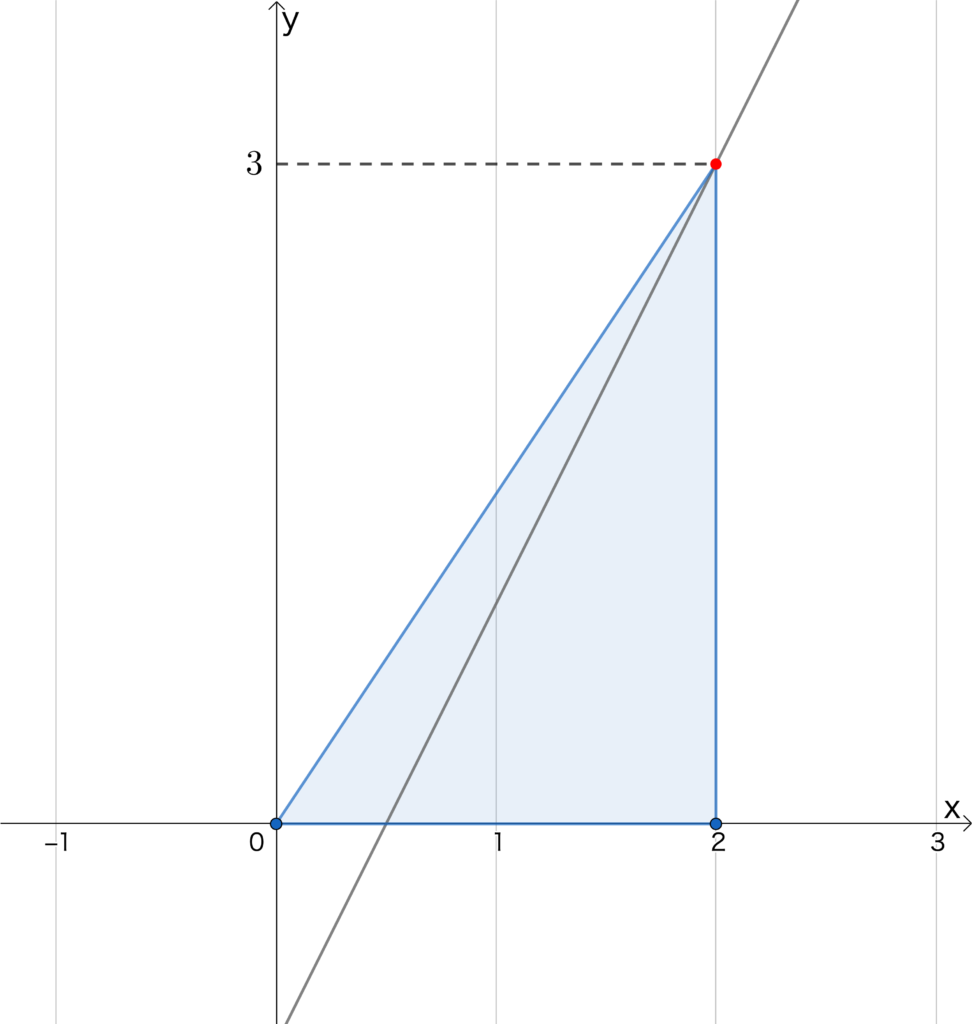
よって、三角形の高さは3であり、面積を$S$とすると$$S=2\times3\times\frac{1}{2}\\=3$$となるのです。

このように、関数のグラフと図形が融合した問題は、

という順番で解きます。
何から手をつけたらいいかわからない時は、とりあえず全ての座標を求めてみるのもいいかもしれません。