円周角の定理の応用問題

3年

問題

難易度☆☆☆

円周角の定理を使う問題ですが、ただ定理を覚えているだけでは解くことができません。

補助線を引くなど、少し頭を捻らなければいけない応用問題です。

応用とはいえおそらくほとんどの問題集に類似問題が出てくるほど、有名な問題だと思います。

今回の文書の中では2パターンの解法を紹介していますが、他の解き方もあります。

ぜひ自分に合った解き方を探してみてください。

円周の一部分のことを弧といいます。

下の図で、円周のうち点Aと点Bの間の部分を弧ABといい\(\stackrel{\huge\frown}{AB}\)と表します。

弧ABを除く円周上に点Pをとるとき、\(\angle APB\)を弧ABに対する円周角といいます。

また、円の中心をOとするとき、\(\angle AOB\)を弧ABに対する中心角といいます。

これらの角に対して成り立つ性質がいくつかあり、まとめて円周角の定理といいます。

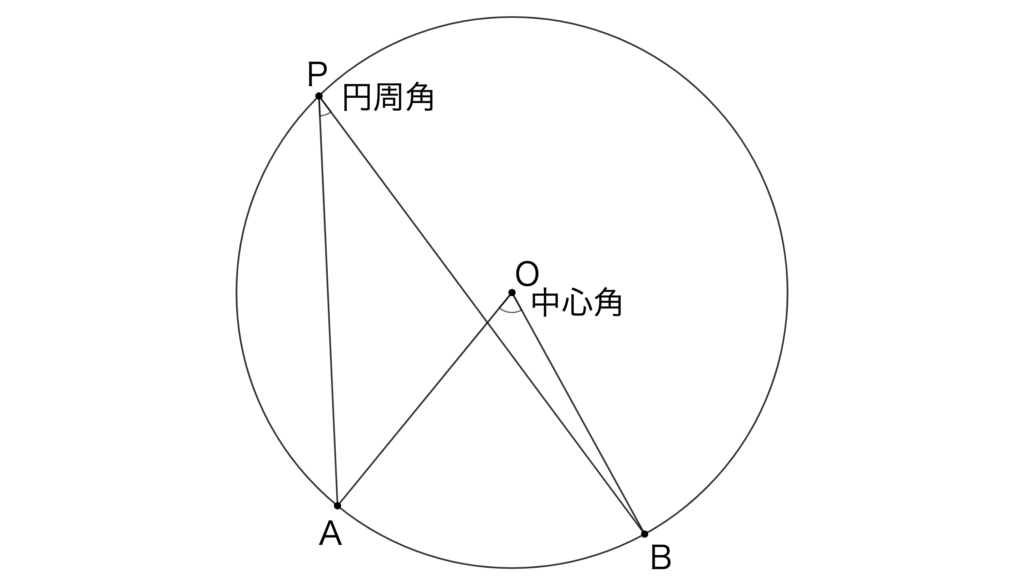
1.中心角は同じ弧に対する円周角の2倍の大きさである

上の図の場合、中心角の方が円周角より大きそうだな、というのはなんとなくお分かりいただけるでしょうか。

実は、どんな円の場合でも中心角は円周角の2倍の大きさになるという性質があります。

2.同じ弧に対する円周角は等しい

複数の円周角が同じ弧に対するものであれば、必ず同じ大きさになります。

下の図で、2つの円周角はどちらも弧ABに対するものなので同じ大きさです。

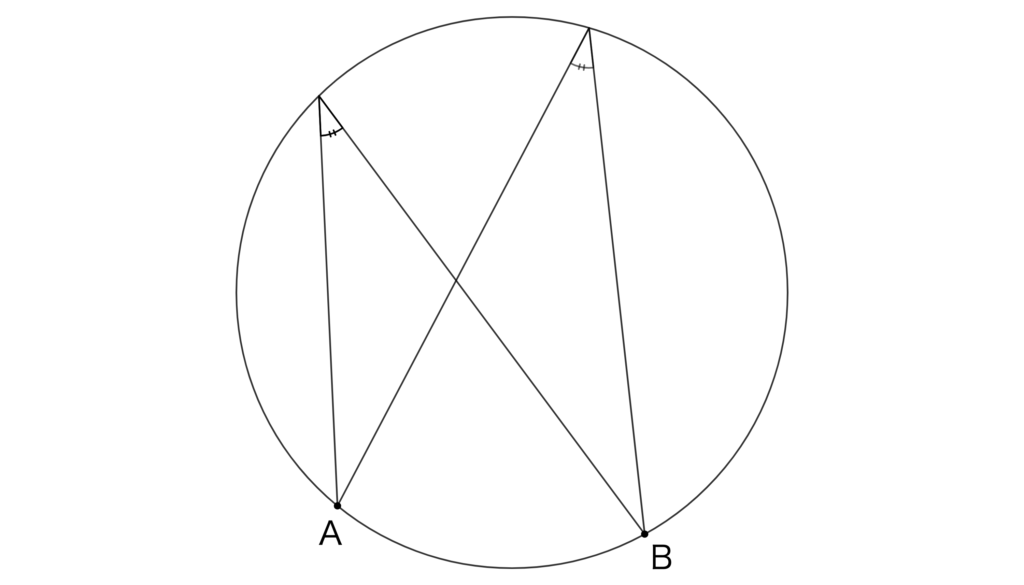
3.半円の弧に対する円周角は直角(\(90^\circ\))

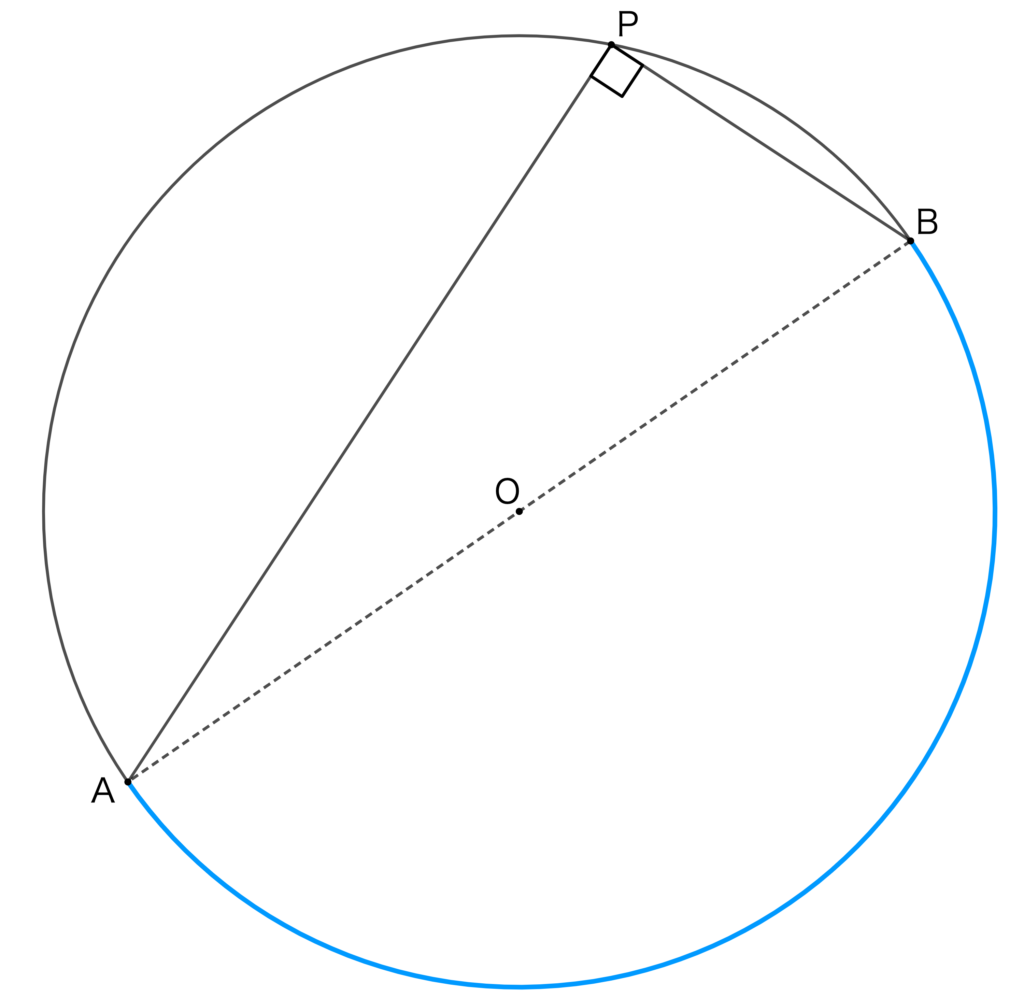
下の図で、線分ABは円の中心を通ってますので、この円の直径ということになります。

そして、青線で示した弧ABは半円です。

半円の弧に対する円周角は必ず\(90^\circ\)であるという性質があります。

半円の弧って何やねん！という方は、正確な表現ではないと思うのですが、「直径に対する円周角は\(90^\circ\)」と覚えても良いと思います。

色々紹介しましたが、数学の公式や性質は覚えている・知っているだけでは何の役にも立ちません。

実際に公式や性質を利用した問題を解いていく中で、どのように使われるのかを理解する必要があります。

円周角の定理も、単純な定理だけにさまざまな工夫を必要とする応用問題が多いので、必ずいくつか問題を解いてみて、実際にどのように使うのかを確かめてみてください。