問題
難易度☆
比例・反比例の理解度を試す問題です。
比例・反比例の式やグラフを覚えているだけではこのような問題を解くことはできません。
それぞれの性質や特徴をしっかりと理解しておく必要があります。
授業
比例
比例は、片方が2倍・3倍…と増加するともう片方も2倍・3倍…となっていくような関係のことです。
\(x\)と\(y\)が比例の関係にあるとき、次のような式で表されます。
$y=ax$
ここで、\(a\)は何らかの定数です。
\(a\)の値によって傾きが変わるものの、比例のグラフには次のような特徴があります。
- 原点を通る
- 直線である

比例の例
1個10円のお菓子を\(x\)個買ったら、金額が\(y\)円になった。
この例の場合、合計金額\(y\)は 1個の値段\(\times\)個数 で\(y=10x\)と表すことができます。
これは、比例の式として紹介した\(y=ax\)の形に当てはまり、比例の式だといえます。
また、個数\(x\)が2倍になると当然値段も2倍になることから、比例の性質を満たしています。
この記事を参考に、この例の比例のグラフを書いてみましょう。
反比例
比例は、片方が2倍・3倍…と増加するともう片方は\frac{1}{2}倍・\frac{1}{3}倍…となっていくような関係のことです。
\(x\)と\(y\)が反比例の関係にあるとき、次のような式で表されます。
$y=\frac{a}{x}$
ここで、\(a\)は何らかの定数です。
また、この式を変形すると\(xy=a\)となることから、反比例の関係にある\(x\)と\(y\)をかけると常に同じ値(\(a\))になることがわかります。
\(a\)の値によって形が変わるものの、反比例のグラフには次のような特徴があります。
- x軸、y軸と交わらない
- 曲線である
また、図のように2つの曲線から構成されるため、双曲線とも呼ばれます。

双曲線は、曲線なので人間が正確に描くことはできません。
双曲線の概形の描き方を次の例で示します。
反比例の例
面積が12の長方形の縦の長さを\(x\)、横の長さを\(y\)とする。
このとき、長方形の面積は\(\text{縦}\times \text{横}\)で表されますので、式は\(xy=12\)となります。
これを変形すると\(y=\frac{12}{x}\)となることから、これは反比例の式です。
双曲線(反比例のグラフ)を描く際は、\(x\)も\(y\)も整数になる点を探すことが重要です。
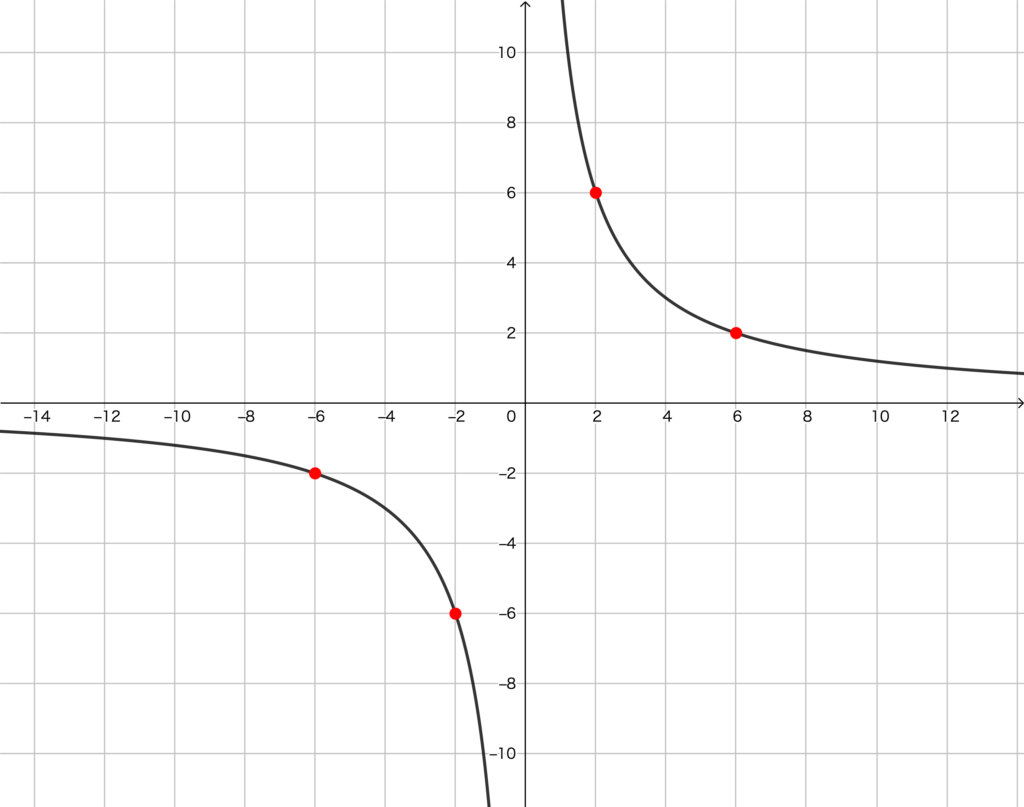
例えばこの例だと、以下の点を通りますよね。
- \((2,6)\)
- \((6,2)\)
- \((-2,-6)\)
- \((-6,-2)\)
この点をプロットし、滑らかな曲線でつなぎます。
ただし、グラフがx軸やy軸と交わらないように注意してください。

 お気に入りに追加
お気に入りに追加 
