問題
難易度☆☆
度数分布表の練習問題です。
方程式や図形問題と比べてあまり重要視されることが少ないように感じますが、割と高い頻度で出題されているようです。
用語の意味をしっかり理解できていれば苦労するレベルの問題は少ないと思うので、練習してしっかり理解しましょう。
授業
統計・資料
何かの値の測定結果などの多くの数字をまとめてわかりやすく分析する分野です。
たくさんの数字の傾向をわかりやすくまとめるため、新しい用語がたくさん出てきます。
また、用語の意味や理解度を確認するような問題も多いため、知らない用語が多いと命取りです。
まずは、以下のような場合を考えて下さい。
以下の表は、あるクラスの全員の数学のテストの点数を表している。 58 88 42 64 66 66 75 81 72 64 72 84 99 91 75 88 57 63 70 57 100 65 57 32 83 65 96 93 42 50 66 71 76 91 44 79 97 43 92 92
皆さんも、テストではそれぞれがバラバラの点数を取るので、それを表にまとめるとこのようになると思います。
しかし、規則正しく並んだわけでもないデータが40個もあります。
この表では一体最高点がいくらなのか、最低点がいくらなのか、全体的にクラスの出来がいいのか悪いのか、などの傾向を、パッとみただけでは判断できません。
そういったことをわかりやすくするため、全ての値からもとまる平均値や中央値といった代表値を使って特徴を考えます。
平均値
皆さんの考えている「平均」です。
「テストの平均点は〜」など、一番馴染みの深い代表値ではないでしょうか。
平均値は、以下の式で求めます。
$$\text{平均値}=\frac{\text{データの合計}}{\text{データの個数}}$$
上の例の場合、「データ」とは58、88、…といった、それぞれの点数のことを表します。そして、そのデータが40人分あるので、「データの個数」は40ですね。
したがって、平均値は
$$\text{平均値}=\frac{\text{データの合計}}{\text{データの個数}}=\frac{58+88+42+…+43+92+92}{40}=\frac{2866}{40}=71.65$$
よって、このクラスの平均点は71.65点となります。
中央値
中央値は、データを順番に並べた時、真ん中にくる値です。メジアンとも言います。
データの個数が奇数個の場合、データを大きい順に並べると真ん中の数がメジアンです。
例えば、 1 3 7 8 10 という5つの数字のうち、真ん中である3番目の数字は7です。
データが偶数個ある場合、真ん中のデータが2つ存在します。
この場合は、この2つの平均をとって、中央値とすることになっています。
例えば上の例の40個のデータを並べると、真ん中の数は20番目と21番目の71と72です。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 32 | 42 | 42 | 43 | 44 | 50 | 57 | 57 | 57 | 58 | 63 | 64 | 64 | 65 | 65 | 66 | 66 | 66 | 70 | 71 | 72 | 72 | 75 | 75 | 76 | 79 | 81 | 83 | 84 | 88 | 88 | 91 | 91 | 92 | 92 | 93 | 96 | 97 | 99 | 100 |
よって、中央値は\(\frac{71+72}{2}=71.5\)です。
最頻値
最頻値は、最も頻繁に現れる値です。モードとも呼ばれます。
モードを求める際も、データを並べ替えるとミスが減ります。
上の例では、57点と66点の生徒が3人ずついて最も多い(他の点数は多くても2人しかいない)ので、モードは57と66です。
度数分布表
下の表は、上の例のテスト結果をもとに作成した度数分布表です。
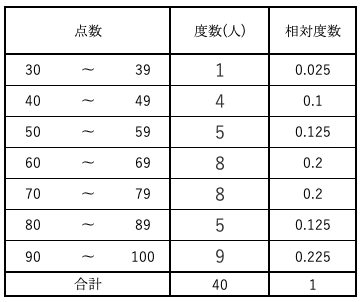
この表の一番左の列に書かれているのは、階級です。
階級とは、いわばデータを整理するために設定するグループのようなものです。
例えば、「30〜39」の階級は、30点から39点のデータが所属するグループだと考えてください。
そして、真ん中の列の度数とは、その階級に所属するデータの数のことです。
「40〜49」の階級の度数が4であるということは、40点から49点をとった人が4人いるということです。
最後に、一番右の列は相対度数を表しています。相対度数の列は無くても度数分布表と呼べますし、他の列がくっついている場合もあります。相対度数は、全体を1としたとき、その階級にどのくらいの割合のデータが所属しているのかを表します。
合計が1なのでわかりにくいかもしれませんが、「60〜69」の階級には相対度数が0.2とあります。
つまり、40人を1とするとそのうち0.2がこの階級に所属していることになります。
合計が1だとわかりにくい場合は、100倍してみてください。
すると合計が100になり、0.2は20になります。
全員を100%とすると、そのうち20%がこの階級に所属していることになります。

 お気に入りに追加
お気に入りに追加 
