問題
難易度☆☆☆☆
毎度の如く、定番問題です。
重なりや回転がある相似図形の面積比を繰り返し計算しないといけないので、自分なりによく整理しながら解かないとうっかりミスを連発する羽目になります。
必ず問題用紙の裏や余白を使って図を描いたり問題の図に描き込んだりしながら落ち着いて解き進めて行きましょう。
授業
相似
同じ形で拡大/縮小のみした図形のことを、相似な図形といいます。
また、拡大/縮小により生まれた大きさの比率を相似比といいます。
例えば図形Aと図形Bが相似の関係にあり、Bの大きさがAの大きさの2倍であれば、AとBの相似比は1:2ということになります。
相似な図形の性質
図の\(\triangle ABC\)と\(\triangle DEF\)は相似な関係で、相似比は1:2です。
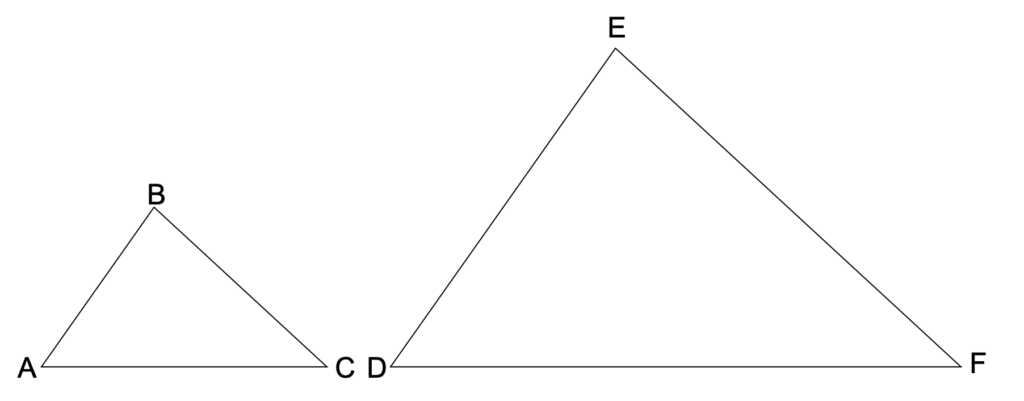
重ねてみると、二つの図形の性質がわかりやすいです。
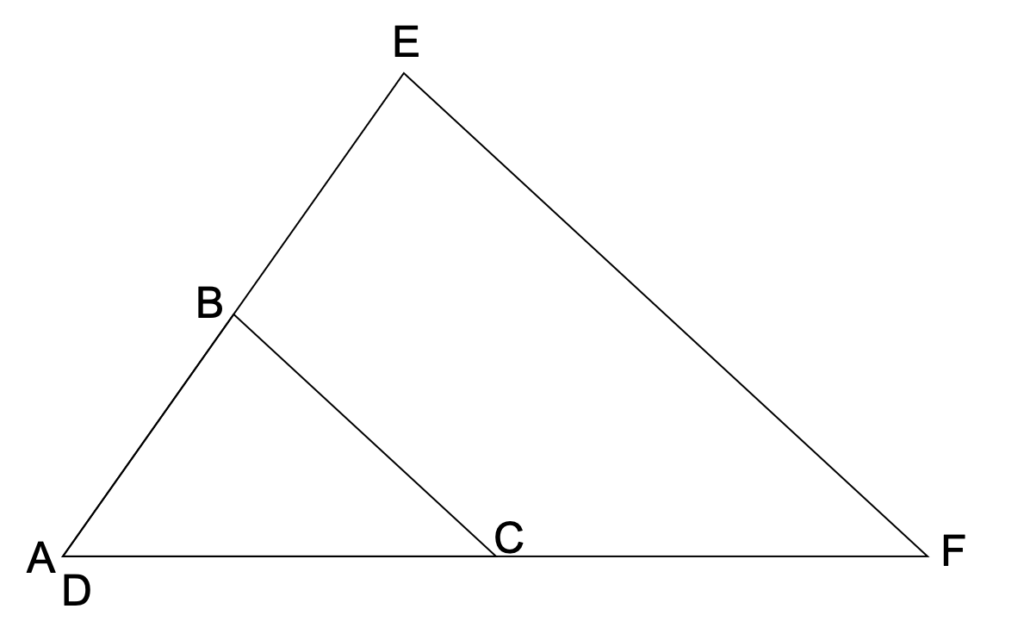
\(AB:AE\)、\(AC:AF\)が\(1:2\)になっています。また、\(\angle BAC=\angle EDF\)になっています。
他の辺や角にも同じ関係があり、一般に相似な図形には次の性質があります。
- 相似な図形の対応する辺の比は全て等しく、その比は相似比に等しい
- 相似な図形の対応する角の大きさは等しい
例えば図形を2倍に拡大すると辺の長さは全て2倍になり、角の大きさは変わらないということです。
相似な図形の面積比
相似な図形では、面積にもある法則があります。
相似な図形の面積比についてはこちらをご覧ください。
三角形の相似証明
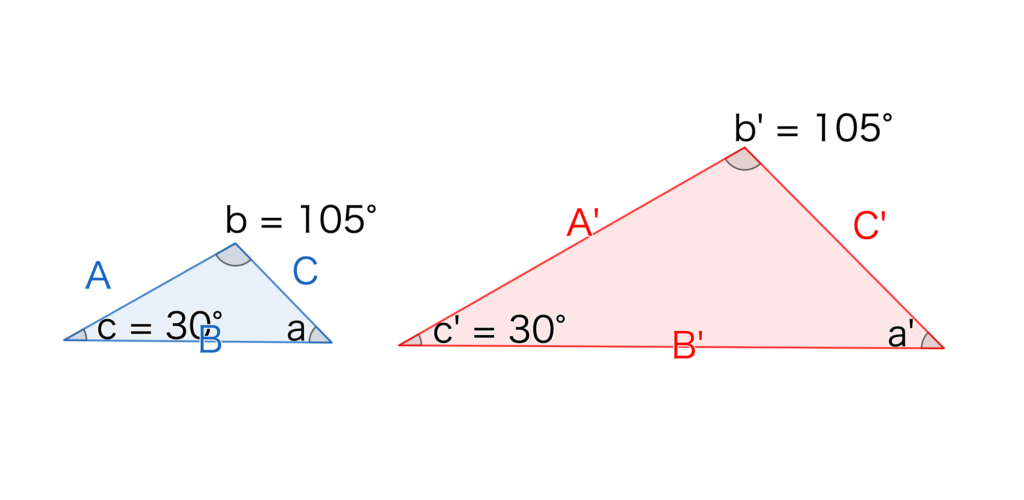
三角形が相似であることを証明するためには、次の3つの相似条件のうちどれかが正しいことをいう必要があります。
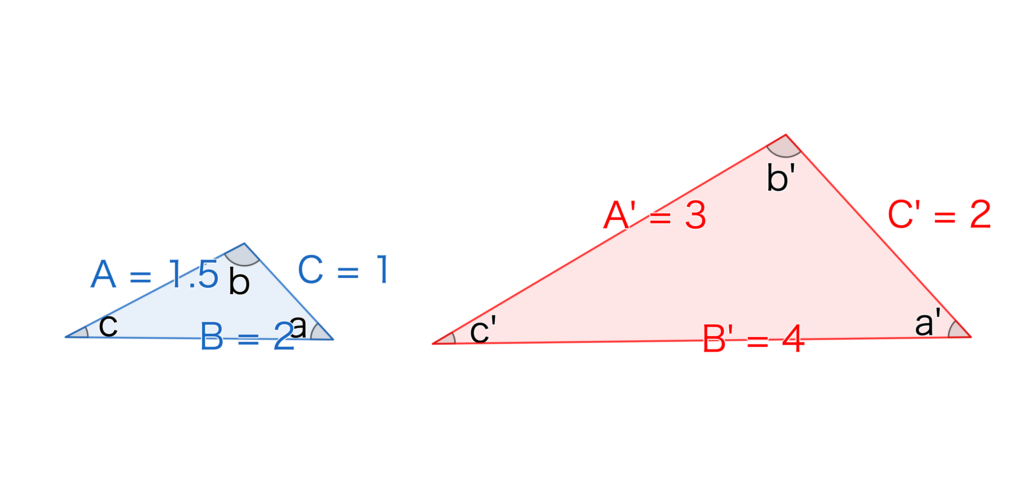
- 3組の辺の比がそれぞれ等しい
図の右の三角形は、全ての辺が左の三角形の2倍になっています。
この場合、右の三角形は左の三角形を2倍に拡大した図形なので相似であることが証明できます。
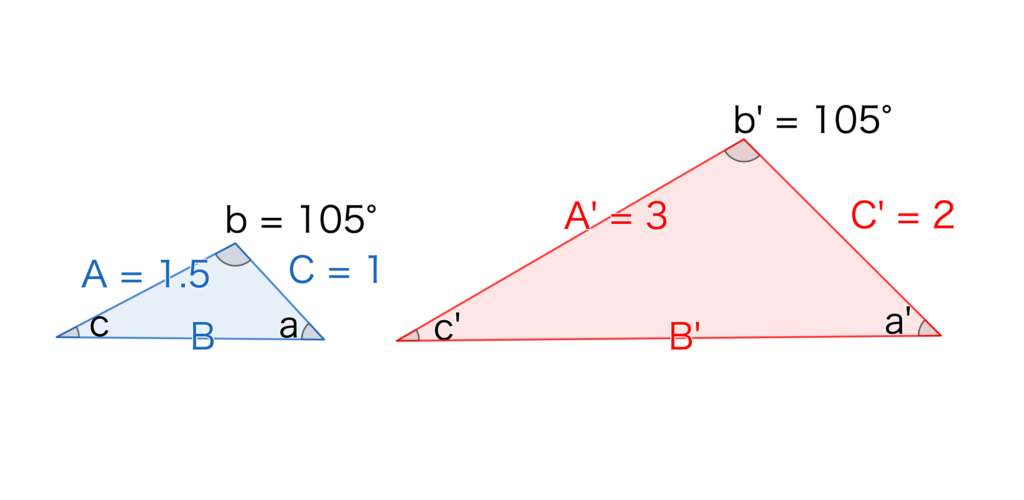
- 2組の辺の比とその間の角がそれぞれ等しい
2つの辺しか長さの比が分からなくても、その間の角が同じであれば、相似であることが証明できます。
- 2組の角がそれぞれ等しい
三角形の内角の和は\(180^\circ\)と決まっているので、2つの角が同じであることが証明できれば自動的にもう1つの角も同じということになります。
全ての角が同じであれば、少なくとも同じ形である(大きさは違うかもしれない)ことがわかるので、相似が証明できます。
相似証明の問題では必ず必要になるので、この3つの条件は覚えておきましょう。
平行線の性質
下の図のように、直線\(l\)と\(m\)に直線\(n\)が交わっています。。
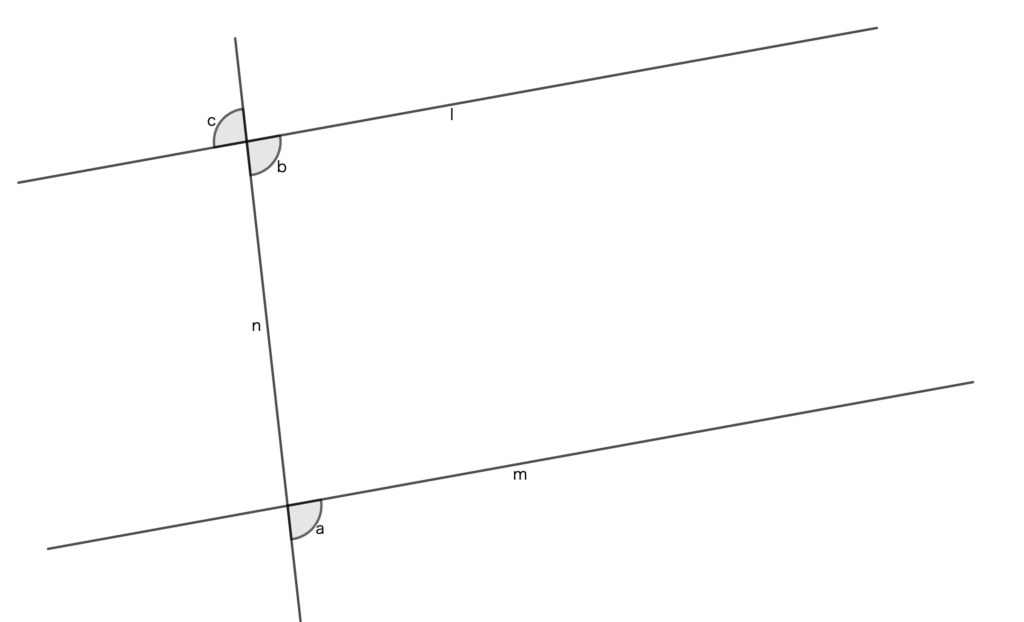
それぞれの交点に対して同じ位置にある角を同位角といいます。
図中では、\(\angle a\)と\(b\)はどちらも交点の右下にあるのであるので同位角であるといえます。
また、同じ交点の反対側にある角を対頂角といいます。
図中の\(\angle b\)と\(\angle c\)がこの関係にあたります。
さらに、同位角の対頂角を錯角と言います。
\(\angle b\)は\(\angle a\)の同位角であり、\(\angle c\)は\(\angle b\)の対頂角なので、\(\angle c\)は\(\angle a\)の同位角の対頂角です。したがって、\(\angle c\)と\(\angle a\)は錯角です。
この中で、対頂角は等しいという性質があります。
さらに、直線\(l\)と直線\(m\)が平行である場合には、同位角と錯角も等しくなります。
- 対頂角は等しい
- 平行線の同位角は等しい
- 平行線の錯角は等しい
合同証明等で本当によく使うので、どのように使われているのかをしっかり理解して使えるようになっておきましょう。

 お気に入りに追加
お気に入りに追加 
