問題
難易度☆☆
一次関数のグラフの式や交点の座標、そしてグラフとx軸からなる三角形の面積を求める問題です。
グラフの式の理解だけでなく、連立方程式を解ける必要があります。
連立方程式は大問1~2の計算問題としてよく出題されます。
また、グラフの式や交点を求めることも入試においては必須級の能力と言えるでしょう。
授業
一次関数の式
一次関数とは、yがxの一次式で表される関数のことです。関数について詳しくはこちらをご覧ください。
一次式というのは、最大次数が1、すなわち変数が最大1回しかかけられていない式です。
例えば、\(x+1\)は\(x\)に何もかかっていないので一次関数ですが、\(x^2+2x+1\)などは\(x^2(=x\times x)\)という項を含んでおり、変数\(x\)が2回かかっているので一次関数ではありません(二次関数といいます)。
また、\(2x+1\)なども、\(x\)にかけられているのは2という定数であり変数ではないので、一次関数です。
一次関数の式は、一般に\(a\)と\(b\)をある定数として\(y=ax+b\)という式で表されます。
\(a\)を変化の割合や傾き、\(b\)を\(y\)切片といいます。
一次関数のグラフ
関数のグラフの意味についてはこちらをご覧ください。
ここでは、一次関数のグラフの描き方を紹介します。
一次関数のグラフは必ず直線になります。したがって、二つの点がわかればその点を結んで伸ばすだけでグラフが描けます。
試しに、\(y=2x-1\)のグラフを描いてみましょう。
1. 2つの点を求める
\(y=2x-1\)の\(x\)に1を代入すると、\(y=2\times 1-1=1\)よりグラフが\((1,1)\)を通ることがわかります。
同様に0を代入すると、\((0,-1)\)を通ることがわかります。
この2つの点をグラフ上にとってみると、
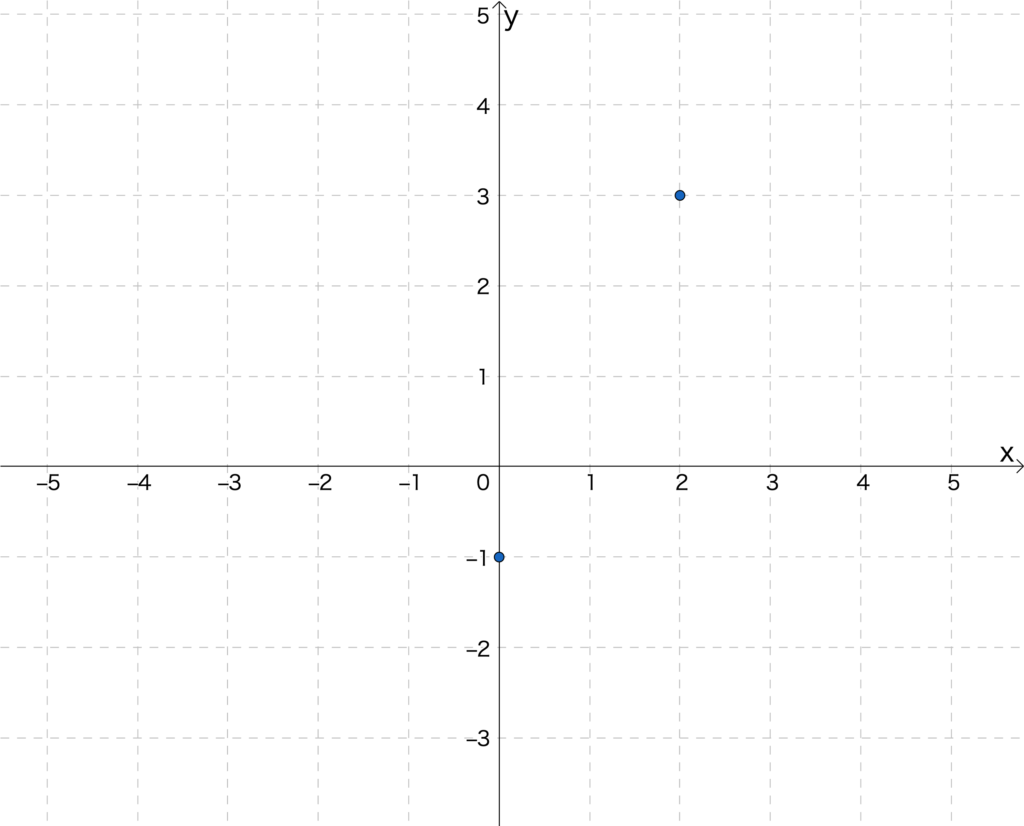
2. 点を直線で結ぶ
一次関数の式は直線であり、今とった2つの点を通るので、とれらを通るように直線を引きます。
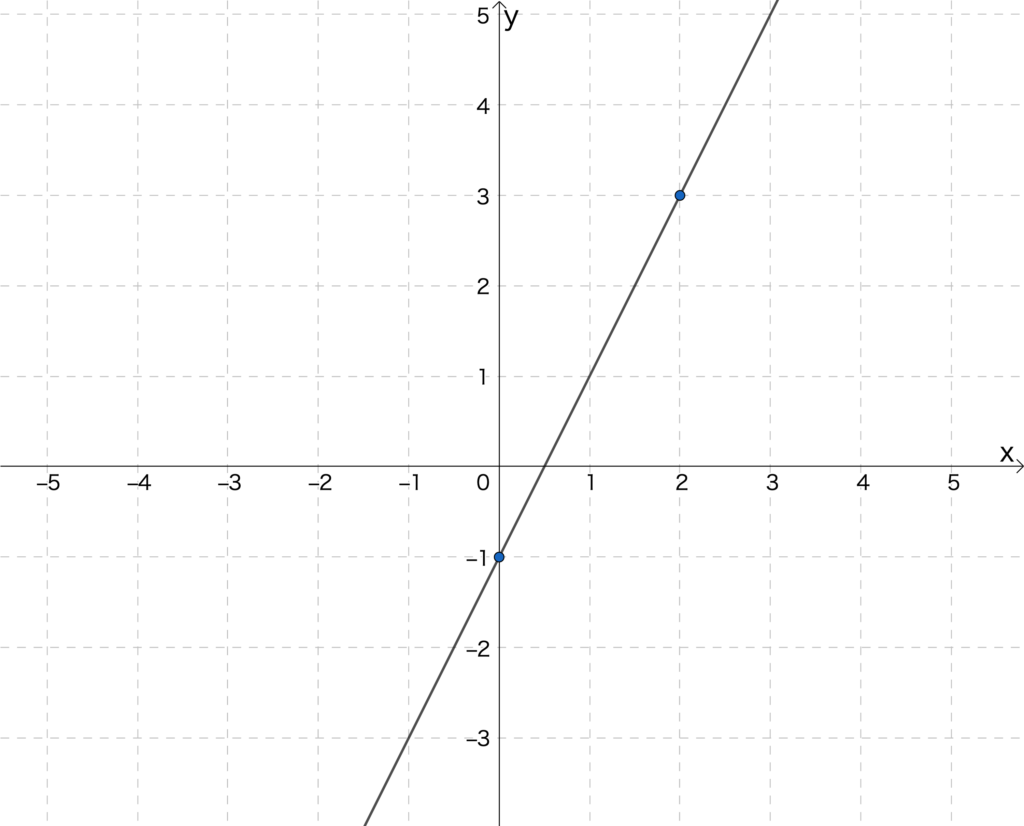
グラフ自体はこれで完成です。
グラフの意味
当然グラフと式には相関があり、式をみてグラフを描くだけでなくグラフを見て式を求めることもできます。
一次関数の式は\(y=ax+b\)の形で求められるので、あとは定数\(a\)と\(b\)の正体を突き止めれば良いのです。
先ほど例に使った\(y=2x-1\)のグラフを見てみましょう(言っちゃったけど、まだ式は知らない体で)。

まず、\(y\)切片\(b\)は簡単に求まります。
一次関数の式\(y=ax+b\)に\(x=0\)を代入してみましょう。
\(a\)がどんな値だったとしても0がかかっているので消えてしまい、\(y=b\)だけが残ります。したがって、\(y\)切片\(b\)は\(x=0\)のときの\(y\)の値であり、上のグラフでは-1です(y軸との交点のyの値)。
傾き\(a\)は\(x\)が1増えたとき\(y\)がいくら増えるかということを表す数値です。
上のグラフでは、\(x\)が2増えたとき\(y\)が4増えてます。
ということは、4を2で割ると\(x\)が1増えたときの\(y\)の増加量が分かります。すなわち、このグラフの傾き\(a\)は2です(もちろん初めから1増えたとき2増えてるでも良いんですがあえてめんどくさい選び方をしてます)。
一般に、一次関数のグラフの傾きは\(\frac{yの増加量}{xの増加量}\) で求まります。
\(a=2\)、\(b=-1\)とわかったので、\(y=ax+b\)に代入して\(y=2x-1\)。
グラフの交点
下の図のように2つのグラフが交わっています。グラフが交わっている点のことを交点といいます。
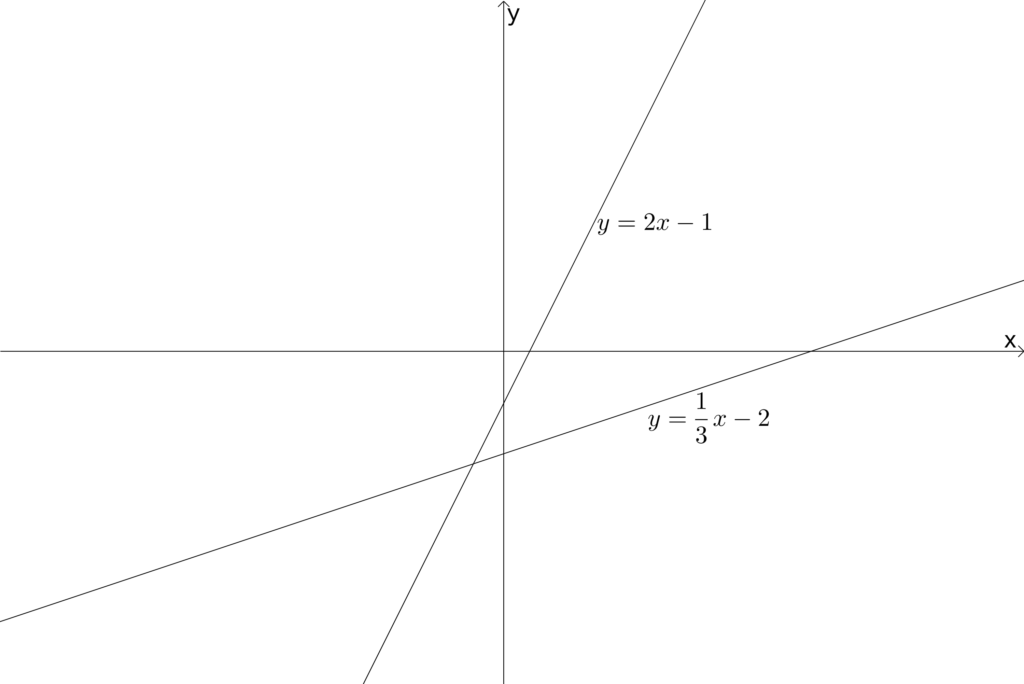
交点では2つのグラフが同じ点を通っています。つまり2つのグラフの\(x\)と\(y\)の値が同じになっています。
その\(x\)と\(y\)をどちらの式に代入しても等式が成り立つべきです。このような\(x\)と\(y\)の組み合わせを見つけるには、連立方程式を使います。
2つのグラフの交点を見つけるには連立方程式と覚えてください。
\(\begin{cases}
y=2x-1… A \\
y=\frac{1}{3}x-2…B
\end{cases}\)
式Aを式Bに代入して
$$2x-1=\frac{1}{3}x-2$$
これを解くと\(x=-\frac{3}{5}\)
Aに代入して
$$y=2\times (-\frac{3}{5})-1$$
これを解いて\(y=-\frac{11}{5}\)
よって交点の座標は\((-\frac{3}{5},-\frac{11}{5})\)
関数のグラフと図形
関数のグラフを辺とする図形の面積の求め方について詳しくはこちらをご覧ください。
連立方程式
この問題では交点を求める場合などに連立方程式が大活躍します。
連立方程式について、詳しくはこちらをご覧ください。

 お気に入りに追加
お気に入りに追加 
